Free NCERT Class 12 Maths Miscelleneous Ex. Ch 7 Solution

Free NCERT Class 12 Maths Miscellaneous Ex. Ch 7 Solution Here

NCERT Class 12 Maths Misc. Ex. ch 7 Solution Q. 1 to Q.23 (Indefinite Integrals)

NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution — Source: Canva AI

Here, you get Free NCERT Class 12 Maths Miscellaneous Ex. Ch 7 Solution

For Class 12th NCERT Maths Ch. 7 EX. 7.1 Solutions Click Here

Q. 1. NCERT Class 12 mathsSolution:

\[
\begin{aligned}
I &= \int \frac{1}{x – x^{3}}\,dx \\\
&= \int \frac{1}{x(1 – x^{2})}\,dx \\\
&= \int \frac{1}{x(1 – x)(1 + x)}\,dx \\\
\frac{1}{x(1 – x)(1 + x)} &= \frac{A}{x} + \frac{B}{1 – x} + \frac{C}{1 + x} \\\
1 &= A(1 – x)(1 + x) + Bx(1 + x) + Cx(1 – x) \\\
A = 1,\;\; B = \frac{1}{2},\;\; C = -\frac{1}{2} \\\
I &= \int \frac{1}{x}\,dx + \frac{1}{2}\int \frac{1}{1 – x}\,dx – \frac{1}{2}\int \frac{1}{1 + x}\,dx \\\
&= \ln|x| + \frac{1}{2}\ln|1 – x| – \frac{1}{2}\ln|1 + x| + C \\\
&= \ln|x| + \frac{1}{2}\ln\left|\frac{1 – x}{1 + x}\right| + C
\end{aligned}
\]

Q.2. NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$ \begin{aligned} I &= \int \frac{dx}{\sqrt{x + a} + \sqrt{x + b}} \\ &= \int \frac{\sqrt{x + a} – \sqrt{x + b}}{(x + a) – (x + b)} dx \\ &= \frac{1}{a – b}\int (\sqrt{x + a} – \sqrt{x + b}) \, dx \\ &= \frac{1}{a – b} \left[\frac{2}{3}(x + a)^{3/2} – \frac{2}{3}(x + b)^{3/2}\right] + c \\ &= \frac{2}{3(a – b)}\left[(x + a)^{3/2} – (x + b)^{3/2}\right] + c \end{aligned} $$

Q.3. NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$ \begin{aligned} I &= \int \frac{dx}{x\sqrt{ax – x^2}} \\ \text{Put } x &= \frac{a}{t} \Rightarrow dx = -\frac{a}{t^2} dt \\ I &= -\int \frac{dt}{a\sqrt{t – 1}} = -\frac{1}{a}\int \frac{dt}{\sqrt{t – 1}} \\ &= -\frac{2}{a}\sqrt{t – 1} + c = -\frac{2}{a}\sqrt{\frac{a}{x} – 1} + c \\ &= \frac{-2}{a}\sqrt{\frac{a – x}{x}} + c \end{aligned} $$

Q.4. NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$ \begin{aligned} I &= \int \frac{dx}{x^2(x^4 + 1)^{3/4}} \\ \text{Put } t &= 1 + \frac{1}{x^4} \Rightarrow dt = -\frac{4}{x^5} dx \\ \Rightarrow \frac{1}{x^5}dx &= -\frac{1}{4} dt \\ I &= -\frac{1}{4}\int t^{-3/4} dt\\ = -\frac{1}{4} \cdot \frac{t^{1/4}}{1/4} + c \\ &= -\left(1 + \frac{1}{x^4}\right)^{1/4} + c\\& = -\frac{(x^4 + 1)^{1/4}}{x} + c \end{aligned} $$

Q.5. NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$ \begin{aligned} I &= \int \frac{dx}{x^{1/3} + x^{1/2}} = \int x^{-1/3}(1 + x^{1/6})^{-1} dx \\ \text{Put } x &= t^6 \Rightarrow dx = 6t^5 dt \\ I &= 6\int \frac{t^5}{t^2(1 + t)}dt = 6\int \frac{t^3}{1 + t} dt \\ &= 6\int \left(t^2 – t + 1 – \frac{1}{1 + t}\right) dt \\ &= 6\left(\frac{t^3}{3} – \frac{t^2}{2} + t\right) – 6\log|1 + t| + c \\ &= 2t^3 – 3t^2 + 6t – 6\log|1 + t| + c \\ &= 2x^{1/2} – 3x^{1/3} + 6x^{1/6} – 6\log|1 + x^{1/6}| + c \end{aligned} $$

Q.6.NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$ \begin{aligned} I &= \int \frac{5x}{(x + 1)(x^2 + 9)} dx \\\ \text{Let } \frac{5x}{(x + 1)(x^2 + 9)} &= \frac{A}{x + 1} + \frac{Bx + C}{x^2 + 9} \\\ \Rightarrow 5x &= A(x^2 + 9) + (Bx + C)(x + 1) \\\ &\Rightarrow (A + B)x^2 + (B + C)x + (9A + C) \\ A &= -\frac{1}{2}, \; B = \frac{1}{2}, \; C = \frac{9}{2} \\\ I &= -\frac{1}{2}\int \frac{dx}{x + 1} + \frac{1}{2}\int \frac{x}{x^2 + 9}dx + \frac{9}{2}\int \frac{dx}{x^2 + 9} \\\ &= -\frac{1}{2}\log|x + 1| + \frac{1}{4}\log|x^2 + 9| + \frac{3}{2}\tan^{-1}\frac{x}{3} + c \end{aligned} $$

Q. 7.NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

\begin{aligned}
\text
I &= \int \frac{\sin x}{\sin (x – a)} \, dx \\
&= \int \frac{\sin (x – a + a)}{\sin (x – a)} \, dx \\
&= \int \frac{\sin (x – a)\cos a + \cos (x – a)\sin a}{\sin (x – a)} \, dx \\
&= \int \cos a \, dx + \sin a \int \cot (x – a) \, dx \\
&= x \cos a + \sin a \ln|\sin (x – a)| + C
\end{aligned}

Q.8.NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

\begin{aligned}
\text{Q.8. Solution:} \
I &= \int \frac{e^{5 \log x} – e^{4 \log x}}{e^{3 \log x} – e^{2 \log x}} \, dx \\
&= \int \frac{x^5 – x^4}{x^3 – x^2} \, dx \quad [\text{As } e^{\log x} = x] \\
&= \int \frac{x^4 (x – 1)}{x^2 (x – 1)} \, dx \\
&= \int x^2 \, dx \\
&= \frac{x^3}{3} + C
\end{aligned}

Q.9.NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$\begin{aligned}
I & =\int \frac{\cos x}{\sqrt{4-\sin ^2 x}} d x \\
& =\int \frac{\cos x d x}{\sqrt{2^2-\sin ^2 x}} \quad \text { put sin } x=t \\
& =\int \frac{d t}{\sqrt{2^2-t^2}} \quad \text { coss } x d x=d t \\
& =\sin ^{-1} \frac{t}{2}+c=\sin ^{-1}(\sin x) / 2+c
\end{aligned}$$

Q.10.NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$
\begin{aligned}
I &= \int \frac{\sin^8 x – \cos^8 x}{1 – 2\sin^2 x \cos^2 x} \, dx \\
&= \int \frac{(\sin^4 x – \cos^4 x)(\sin^4 x + \cos^4 x)}{1 – 2\sin^2 x \cos^2 x} \, dx \\
&= \int \frac{(\sin^2 x – \cos^2 x)(\sin^2 x + \cos^2 x)\left[(\sin^2 x + \cos^2 x)^2 – 2\sin^2 x \cos^2 x\right]}{1 – 2\sin^2 x \cos^2 x} \, dx \\
&= \int \frac{(\sin^2 x – \cos^2 x)(1)(1 – 2\sin^2 x \cos^2 x)}{1 – 2\sin^2 x \cos^2 x} \, dx \\
&= \int (\sin^2 x – \cos^2 x) \, dx \\
&= -\frac{1}{2}\sin 2x + C \quad [\text{Since } \sin^2 x + \cos^2 x = 1]
\end{aligned}
$$

Q.11. NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

\begin{aligned}
I & =\int \frac{1}{\cos (x+a) \cos (x+b)} d x\left[\begin{array}{c}
\text { We can not expand denominator and } \\
\text { one term need to be eliminated }
\end{array}\right] \\
& =\frac{1}{\sin (a-b)} \int \frac{\sin [(x+a)-(x+b)]} {\cos (x+a) \cos (x+b)} \\
& =\frac{1}{\sin (a-b)} \int\left[\frac{\sin (x+a) \cos (x+b)} {\cos (x+a) \cos (x+b)}-\frac{\cos (x+a) \sin (x+b)} {\cos (x+a) \cos (x+b)}\right] d x \\
& =\frac{1}{\sin (a-b)} \int[\tan (x+a)-\tan (x+b)] dx\\
&=\log{\sec(x+a)}-\log{\sec(x+b)}+C\\
&=\log[{sec(x+a)}/{sec(x+b)}]+C
\end{aligned}

Q. 12. NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$
\text { Q.12. } I=\int \frac{x^3 d x}{\sqrt{1-x^8}}
$$

Solution: put x^4=t
$$
\begin{aligned}
& \Rightarrow 4 x^3 d x=d t \text { (d.br.w.r.t.x) } \\
& \Rightarrow x^3 d x=\frac{d t}{4} \\
I & =\frac{1}{4} \int \frac{d t}{\sqrt{1-t^2}}=\frac{1}{4} \sin ^{-1} t+c \\
& =\frac{1}{4} \sin ^{-1}\left(x^4\right)+c
\end{aligned}
$$

Q. 13. NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$
I = \int \frac{e^{x}}{(1 + e^{x})(2 + e^{x})} \, dx
$$

$$
\text{Let } e^{x} = t
$$

$$
\text{Then } e^{x} \, dx = dt
$$

$$
I = \int \frac{dt}{(1 + t)(2 + t)}
$$

$$
= \int \left( \frac{1}{1 + t} – \frac{1}{2 + t} \right) dt
$$

$$
\text{(You may also write } \frac{1}{(1 + t)(2 + t)} = \frac{A}{1 + t} + \frac{B}{2 + t}
\text{ and solve for } A, B \text{.)}
$$

$$
I = \ln(1 + t) – \ln(2 + t) + C
$$

$$
I = \ln!\left( \frac{1 + t}{2 + t} \right) + C
$$

$$
\text{Substitute back } t = e^{x}:
\quad I = \ln!\left( \frac{1 + e^{x}}{2 + e^{x}} \right) + C
$$

Q.14. NCERT Class 12 maths Misc. Ex. Ch 7 Solution:

$$
I = \int \frac{1}{(x^2 + 1)(x^2 + 4)} \, dx
$$

$$
\text{Let } y = x^2
$$

$$
\frac{1}{(y + 1)(y + 4)} = \frac{A}{y + 1} + \frac{B}{y + 4}
$$

$$
1 = A(y + 4) + B(y + 1)
$$

$$
1 = (A + B)y + (4A + B)
$$

$$
A + B = 0, \quad 4A + B = 1
$$

$$
\Rightarrow A = \frac{1}{3}, \quad B = -\frac{1}{3}
$$

$$
\frac{1}{(y + 1)(y + 4)} = \frac{1}{3} \cdot \frac{1}{y + 1} – \frac{1}{3} \cdot \frac{1}{y + 4}
$$

$$
I = \frac{1}{3} \int \frac{1}{x^2 + 1} \, dx – \frac{1}{3} \int \frac{1}{x^2 + 4} \, dx
$$

$$
I = \frac{1}{3} \tan^{-1} x – \frac{1}{6} \tan^{-1} \left( \frac{x}{2} \right) + C
$$

Q. 15.NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution

$$
I = \int \cos^{3}x \, e^{\ln(\sin x)} \, dx
$$

$$
\text{Since } e^{\ln x} = x, \text{ we have } e^{\ln(\sin x)} = \sin x
$$

$$
\Rightarrow \ I = \int \cos^{3}x \, \sin x \, dx
$$

$$
= \int \cos^{2}x \, \sin x \, \cos x \, dx
$$

$$
= \int (1 – \sin^{2}x) \, \sin x \, \cos x \, dx
$$

$$
\text{Let } \sin x = t \Rightarrow \cos x \, dx = dt
$$

$$
I = \int (1 – t^{2}) \, t \, dt
$$

$$
= \int t \, dt – \int t^{3} \, dt
$$

$$
= \frac{t^{2}}{2} – \frac{t^{4}}{4} + C
$$

$$
\text{Substitute back } t = \sin x:
\quad I = \frac{\sin^{2}x}{2} – \frac{\sin^{4}x}{4} + C
$$

Q. 16. class 12 ncert maths miscellaneous ex ch7

$$
I = \int e^{3 \ln x} \, (x^{4} + 1)^{-1} \, dx
$$

$$
= \int e^{\ln x^{3}} \, (x^{4} + 1)^{-1} \, dx
$$

$$
= \int \frac{x^{3}}{x^{4} + 1} \, dx
$$

$$
\text{Let } x^{4} + 1 = t
$$

$$
\text{Then } \frac{d}{dx}(x^{4} + 1) = 4x^{3} \Rightarrow 4x^{3} \, dx = dt
$$

$$
\Rightarrow x^{3} \, dx = \frac{dt}{4}
$$

$$
I = \frac{1}{4} \int \frac{dt}{t}
$$

$$
I = \frac{1}{4} \ln t + C
$$

$$
\text{Substitute back } t = x^{4} + 1:
\quad I = \frac{1}{4} \ln (x^{4} + 1) + C
$$

Q.17. class 12 ncert maths miscellaneous ex ch7

$$
I = \int f'(ax + b) \, [\,f(ax + b)\,]^n \, dx
$$

$$
\text{Let } f(ax + b) = t
$$

$$
\text{Then, differentiating w.r.t. } x, \quad f'(ax + b) \, dx = dt
$$

$$
\Rightarrow I = \int t^n \, dt
$$

$$
I = \frac{t^{n+1}}{n + 1} + C
$$

$$
\text{Substitute back } t = f(ax + b):
\quad I = \frac{[\,f(ax + b)\,]^{n+1}}{n + 1} + C
$$

Q. 18. class 12 ncert maths miscellaneous ex ch7

$$
I = \int \frac{1}{\sqrt{\sin^{3}x \, \sin(x + \alpha)}} \, dx
$$

$$
\sin^{3}x \, \sin(x + \alpha)
= \sin^{3}x \, (\sin x \cos \alpha + \cos x \sin \alpha)
$$

$$
= \sin^{4}x \, (\cos \alpha + \cot x \sin \alpha)
$$

$$
\Rightarrow I = \int \frac{1}{\sqrt{\sin^{4}x (\cos \alpha + \cot x \sin \alpha)}} \, dx
$$

$$
= \int \frac{1}{\sin^{2}x \, \sqrt{\cos \alpha + \cot x \sin \alpha}} \, dx
$$

$$
= \int \frac{\csc^{2}x}{\sqrt{\cos \alpha + \cot x \sin \alpha}} \, dx
$$

$$
\text{Let } \cos \alpha + \cot x \sin \alpha = t
$$

$$
\text{Then } \frac{d}{dx}(\cos \alpha + \cot x \sin \alpha)
= -\csc^{2}x \sin \alpha
$$

$$
\Rightarrow \csc^{2}x \, dx = -\frac{1}{\sin \alpha} \, dt
$$

$$
I = -\frac{1}{\sin \alpha} \int \frac{dt}{\sqrt{t}}
$$

$$
I = -\frac{2}{\sin \alpha} \sqrt{t} + C
$$

$$
\text{Substitute back } t = \cos \alpha + \cot x \sin \alpha:
\quad\\ I = -\frac{2}{\sin \alpha} \sqrt{\frac{\sin(x + \alpha)}{\sin x}} + C
$$

Q. 19. class 12 ncert maths miscellaneous ex ch7

$$
\begin{aligned}
I &= \int \sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}\,dx \
\text{Put } x &= \cos^{2}\theta
\end{aligned}
$$

$$
\frac{dx}{d\theta}=2\cos\theta(-\sin\theta)=-2\sin\theta\cos\theta
$$

$$
dx=-2\sin\theta\cos\theta\,d\theta
$$

$$
I=\int \sqrt{\frac{1-\cos\theta}{1+\cos\theta}}\;(-2\sin\theta\cos\theta)\,d\theta
$$

$$
1-\cos\theta=2\sin^{2}!\left(\frac{\theta}{2}\right), \qquad
1+\cos\theta=2\cos^{2}!\left(\frac{\theta}{2}\right)
$$

$$
I=-2\int \frac{\sin(\theta/2)}{\cos(\theta/2)}\,\sin\theta\cos\theta\,d\theta
$$

$$
I=-2\int 2\sin^{2}!\left(\frac{\theta}{2}\right)\cos\theta\,d\theta
$$

$$
I=-2\int (1-\cos\theta)\cos\theta\,d\theta
$$

$$
I=-2\int \cos\theta\,d\theta \;+\; 2\int \cos^{2}\theta\,d\theta
$$

$$
\cos^{2}\theta=\frac{1+\cos 2\theta}{2}
$$

$$
I=-2\sin\theta+\theta+\frac{1}{4}\sin 2\theta+C
$$

$$
\cos\theta=\sqrt{x},\qquad \sin\theta=\sqrt{1-x},\qquad
\theta=\arccos(\sqrt{x}),\qquad
\sin 2\theta=2\sqrt{x(1-x)}
$$

$$
I=-2\sqrt{1-x}+\arccos(\sqrt{x})+\frac{1}{2}\sqrt{x(1-x)}+C
$$

Q. 20. class 12 ncert maths miscellaneous ex ch7

$$
I = \int \frac{2 + \sin 2x}{1 + \cos 2x} \, e^{x} \, dx
$$

$$
= \int \frac{2 + 2\sin x \cos x}{2\cos^{2}x} \, e^{x} \, dx
$$

$$
= \int \left[ \frac{2}{2\cos^{2}x} + \frac{2\sin x \cos x}{2\cos^{2}x} \right] e^{x} \, dx
$$

$$
= \int \left( \sec^{2}x + \tan x \right) e^{x} \, dx
$$

$$
I = \int \sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}\,dx \
\text{Put } x = \cos^{2}\theta
$$

$$
I = e^{x} f(x) + C
$$

$$
I = e^{x} \tan x + C
$$

Q. 21. Class 12 ncert maths miscellaneous ex ch7

$$
I = \int \frac{x^{2} + x + 1}{(x + 1)^{2}(x + 2)} \, dx
$$

We can express it as:
$$
\frac{x^{2} + x + 1}{(x + 1)^{2}(x + 2)}
= \frac{A}{x + 1} + \frac{B}{(x + 1)^{2}} + \frac{C}{x + 2}
$$

Multiply through by ( (x + 1)^{2}(x + 2) ):
$$
x^{2} + x + 1 = A(x + 1)(x + 2) + B(x + 2) + C(x + 1)^{2}
$$

Now, substitute convenient values of ( x ):

For ( x = -1 ): ( 1 = B )
For ( x = -2 ): ( 3 = C )
For ( x = 0 ): ( 1 = 2A + 2B + C )

Substitute ( B = 1 ) and ( C = 3 ):
$$
1 = 2A + 2(1) + 3 \Rightarrow 1 = 2A + 5
$$
$$
\Rightarrow A = -2
$$

Hence,
$$
I = \int \frac{-2}{x + 1} \, dx + \int \frac{1}{(x + 1)^{2}} \, dx \\+ \int \frac{3}{x + 2} \, dx
$$

Integrate each term:
$$
I = -2\ln|x + 1| – \frac{1}{x + 1} + 3\ln|x + 2| + C
$$

Q.22. class 12 ncert maths miscellaneous ex ch7

$$
I = \int \tan^{-1}!\sqrt{\frac{1 – x}{1 + x}} \, dx
$$

Let ( x = \cos 2\theta ).

Then,
$$
\frac{dx}{d\theta} = -2\sin 2\theta
\quad \Rightarrow \quad
dx = -2\sin 2\theta \, d\theta
$$

Substitute into the integral:
$$
I = \int \tan^{-1}!\sqrt{\frac{1 – \cos 2\theta}{1 + \cos 2\theta}} \, (-2\sin 2\theta) \, d\theta
$$

Simplify using ( 1 – \cos 2\theta = 2\sin^{2}\theta ) and ( 1 + \cos 2\theta = 2\cos^{2}\theta ):
$$
I = \int \tan^{-1}!\sqrt{\frac{2\sin^{2}\theta}{2\cos^{2}\theta}} \, (-2\sin 2\theta) \, d\theta
$$

$$
I = \int \tan^{-1}!\left(\frac{\sin\theta}{\cos\theta}\right) (-2\sin 2\theta) \, d\theta\\
= \int \tan^{-1}(\tan\theta) (-2\sin 2\theta) \, d\theta\\
$$

$$
I = -2 \int \theta \sin 2\theta \, d\theta
$$

NCERT Class 12 Maths Miscellaneous Ex. Ch 7 Solution

Q.23.class 12 ncert maths miscellaneous ex ch7

$$
I = \int \frac{\sqrt{x^{2}+1}\,\left[\log(x^{2}+1)-2\log x\right]}{x^{4}}\,dx
$$

Rewrite the integrand:

$$
I = \int \frac{\sqrt{\frac{x^{2}+1}{x^{2}}}\,\log!\left(\frac{x^{2}+1}{x^{2}}\right)}{x^{3}}\,dx
$$

Put

$$
t = 1 + \frac{1}{x^{2}}
$$

Differentiate:

$$
dt = -\frac{2}{x^{3}}\,dx
\quad\Rightarrow\quad
dx = -\frac{x^{3}}{2}\,dt
$$

Then:

$$
I = \int \sqrt{t}\,\log t\;dt
$$

Integrate by parts:

$$
\int \sqrt{t}\,\log t\;dt
= \frac{2}{3}t^{3/2}\log t – \frac{4}{3}t^{1/2} + C
$$

Back-substitute t = 1 + \frac{1}{x^{2}}.

$$
I = \frac{2}{3}\left(1+\frac{1}{x^{2}}\right)^{3/2}\log\left(1+\frac{1}{x^{2}}\right) – \frac{4}{3}\sqrt{1+\frac{1}{x^{2}}} + C
$$

NCERT Class 12 maths Miscelleneous Ex. Ch 7 Solution for Definite Integrals Q. 24 to Q. 40

NCERT Class 12 Maths Misc. Ex. Ch 7 (Definite Integrals)

Q. 24. NCERT Class 12 Maths Misc. Ex. Ch 7 solution

$$
I=\int_{\pi/2}^{\pi} e^{x}\left(\frac{1}{2}\csc^{2}\frac{x}{2}-\cot\frac{x}{2}\right)\,dx \\
\text{Let } f(x)=-\cot\frac{x}{2},\ f'(x)=\frac{1}{2}\csc^{2}\frac{x}{2} \\
I=\int e^{x}(f'(x)+f(x))\,dx \\
I=-e^{x}\cot\frac{x}{2}\Big|_{\pi/2}^{\pi} \\
I=-\left(e^{\pi}\cot\frac{\pi}{2}-e^{\pi/2}\cot\frac{\pi}{4}\right) \\
\cot\frac{\pi}{2}=0 ,\ \cot\frac{\pi}{4}=1 \\
I=e^{\pi/2}
$$

Q. 25 NCERT Class 12 Maths Misc. Ex. Ch 7 solution

\begin{align}
\int_0^\frac\pi{4}\frac{sinxcosx}{cos^4x+sin^4x}{dx}
\end{align}-
\begin{align}
&=\int_0^\frac\pi{4}\frac{sinxcosx}{{(1-sin^2x)^2}+{sin^4x}}dx\
& Put sin^2x=t\
& Differentiating w.r.t. x\
& 2sinxcosx=\frac{dx}{dt}\
&sinxcosxdx=\frac{1}{2}dt\
when &\;x=0, t=0\
&when \;x=\frac{\pi}{4},t=\frac{1}{2}\
&I=\frac{1}{2}\int_0^\frac{1}{2}\frac{dt}{(1-t)^2+t^2}\
&=\frac{1}{2}\int_0^\frac{1}{2}\frac{dt}{2t^2-2t+1}\
&=\frac{1}{4}\int_0^\frac{1}{2}\frac{dt}{t^2-t+\frac{1}{2}}\
&=\frac{1}{4}\int_0^\frac{1}{2}\frac{dt}{(t-\frac{1}{2})^2+\frac{1}{2}^2}\
&=\frac{1}{4}.2[tan^-1(2t-1)]_0^\frac{1}{2}\
&=\frac{1}{2}[0-(-\frac{\pi}{4})]\
&=\frac{\pi}{8}
\end{align}

Q. 26. NCERT Class 12 Maths Misc. Ex. Ch 7 solution

$$
I=\int_{0}^{\frac{\pi}{2}} \frac{\cos ^{2} x d x}{\cos ^{2} x+4 \sin ^{2} x}
$$

Dividing numerator and Denominator by cos^4x

$$
\begin{aligned}
I & =\int_{0}^{\frac{\pi}{2}} \frac{\sec ^{2} x d x}{\sec ^{2} x+4 \sec ^{2} x \tan ^{2} x} \
& =\int_{0}^{\frac{\pi}{2}} \frac{\sec ^{2} x}{\left(1+\tan ^{2} x\right)+4\left(1+\tan ^{2} x\right)}-\tan ^{2} x
\end{aligned}
$$

Put tan x=t

$$
\begin{aligned}
& \text { Diff.w.r.t.x } \\
& \sec ^{2} x d x=d t \\
& \text { when } x=0, t=0 \\
& x=\frac{\pi}{2}, t=\infty \\
& =\int \frac{d t}{11+t^{2}+4\left(1+t^{2}\right) t^{2}}
\end{aligned}
$$

$$
\begin{aligned}
\cdots \perp & -\int_{0} \frac{}{\left(1+t^{2}\right)+4\left(1+t^{2}\right) t^{2}} \\
= & \int_{0}^{\infty} \frac{d t}{\left(1+t^{2}\right)\left(1+4 t^{2}\right)} \\
\frac{1}{\left(1+t^{2}\right)\left(1+4 t^{2}\right)} & =\frac{A}{1+t^{2}}+\frac{B}{1+4 t^{2}} \\
\Rightarrow 1 & =A\left(1+4 t^{2}\right) +B\left(1+t^{2}\right) \\
\Rightarrow 1 & =(A+B)+(4 A+B) t^{2}\\
\end{aligned}
$$

Equating both sides, we get

1=A+B… (1) and 4A+B=0… (2)

Fram (2) \quad B=-4 A

From (1) & (2)

A=-1/3 and B=4/3

\[
\begin{aligned}
A &= -\frac{1}{3}, \quad B = \frac{4}{3} \\[6pt]
\text{Therefore, } I &= -\frac{1}{3}\int_{0}^{\infty}\frac{1}{1+t^{2}}\,dt
+ \frac{4}{3}\int_{0}^{\infty}\frac{1}{1+(2t)^{2}}\,dt \\[6pt]
&= -\frac{1}{3}\left[\tan^{-1} t\right]_{0}^{\infty}
+ \frac{4}{3}\cdot \frac{\left[\tan^{-1}(2t)\right]_{0}^{\infty}}{2} \\[6pt]
&= -\frac{1}{3}\left(\frac{\pi}{2} – 0\right)
+ \frac{2}{3}\left(\frac{\pi}{2} – 0\right) \\[6pt]
&= -\frac{\pi}{6} + \frac{\pi}{3} = \frac{\pi}{6}
\end{aligned}
\]

Q. 27. NCERT Class 12 Maths Misc. Ex. Ch 7 solution

\begin{align}
\int_\frac{\pi}{6}^\frac{\pi}{3}\frac{sinx+cosx}{\sqrt{sin2x}}dx\
writing \ sin2x=1-(sinx-cosx)^2\
\end{align}
\begin{align}
I=\int_\frac{\pi}{6}^\frac{\pi}{3}\frac{sinx+cosx}{\sqrt{(1-(sinx-cosx)^2}}dx\
\end{align}

Let sin x – cos x = t

Differentiating w.r.t. x,
$$
(\cos x + \sin x)\,dx = dt
$$

when x=\frac{\pi}{6}, t=\frac{-(\sqrt3-1)}{2}\
x=\frac{\pi}{3}, t=\frac{\sqrt(3)-1)}{2}\

Hence,
$$
I = \int_{(1-\sqrt{3})/2}^{(\sqrt{3}-1)/2} \frac{dt}{\sqrt{1 – t^2}}
$$

$$
I = \left[ \sin^{-1} t \right]_{(1-\sqrt{3})/2}^{(\sqrt{3}-1)/2}
$$

$$
\boxed{I = 2 \sin^{-1}!\left(\frac{\sqrt{3}-1}{2}\right)}
$$

Q.28. NCERT Class 12 Maths Misc. Ex. Ch 7 solution

$$
\begin{aligned}
I & =\int_0^1 \frac{1}{\sqrt{1+x}-\sqrt{x}} \\
& =\int_0^1 \frac{\sqrt{1+x}+\sqrt{x}}{(\sqrt{1+x}-\sqrt{x})(\sqrt{1+x}+\sqrt{x})} d x \\
& =\int_0^1 \frac{\sqrt{1+x}+\sqrt{x}}{1+x-x} d x
\end{aligned}
$$

\begin{aligned}= & \int_0^1(1+x)^{\frac{1}{2}} d x+\int_0^1 x^{\frac{1}{2}} d x \\ = & \frac{2}{3}\left[(1+x)^{3 / 2}\right]_0^1+\frac{2}{3}\left[x^{3 / 2}\right]_0^1 \\ = & \frac{2}{3}\left[(1+1)^{3 / 2}-(1+0)^{3 / 2}\right] \\ & +\frac{2}{3}\left[(1)^{3 / 2}-(0)^{3 / 2}\right]\end{aligned}

$$
\begin{aligned}
& =\frac{2}{3}\left[2^{3 / 2}-1\right]+\frac{2}{3}[1] \
& =\frac{2}{3}[2 \sqrt{2}-x+x] \
& =\frac{4 \sqrt{2}}{3}
\end{aligned}
$$

Q.29.NCERT Class 12 Maths Misc. Ex. Ch 7 (Definite Integrals)

$$
\begin{aligned}
& I=\int_0^{\frac{\pi}{4}} \frac{\sin x+\cos x d x}{9+16 \sin 2 x} \\
& \sin 2 x=1-(\sin x-\cos x)^2 \\
& \ I=\int_0^{\frac{\pi}{4}} \frac{\sin x+\cos x}{9+16\left[1-(\sin x-\cos x)^2\right]} \\
& P u t \sin x-\cos x=t \\
& \Rightarrow \cos x+\sin x=\frac{d u}{d x} \\
& \Rightarrow(\sin x+\cos x) d x=d t \\
& f-a r=\frac{\pi}{4}, t=0 \\
& x=0, t=-1 \\
& 0 \\
& \ I=\frac{d t}{9+16\left(1-t^2\right)}
\end{aligned}
$$

$$
\begin{aligned}
& =\int_{-1}^0 \frac{d t}{25-16 t^2} \\
& =\int_{-1}^0 \frac{d t}{16\left[\frac{25}{16}-t^2\right]} \\
& =\frac{1}{16} \int_{-1}^0 \frac{d t}{\left(\frac{5}{4}\right)^2-t^2} \\
& =\frac{1}{16} \cdot \frac{1}{2} \cdot\left[\log \frac{5}{4}+\frac{5}{\frac{5}{4}}+t\right. \\
& =\frac{1}{16} \cdot \frac{2}{5}\left[\log \frac{5+4 t}{5-4 t}\right]_{-1}^0 \\
& =\frac{1}{40}\left[\log 1-\log \frac{1}{9}\right] \\
& =\frac{1}{40}[\log 1-\log 1+\log 9] \\
& =\frac{1}{40} \log 9 .
\end{aligned}
$$

Q. 30.NCERT Class 12 Maths Misc. Ex. Ch 7 (Definite Integrals)

$$
\begin{aligned}
I & =\int_0^{\frac{\pi}{2}} \sin 2 x \tan ^{-1}(\sin x) d x \\
& =\int_0^{\frac{\pi}{2}} 2 \sin x \cos x \tan ^{-1}(\sin x) d x \\
& =2 \int_0^{\frac{\pi}{2}} \sin x \tan ^{-1}(\sin x) \cdot \cos x d x
\end{aligned}
$$

Put \sin x=t
Diff. w.r.t.x
$$
\begin{aligned}
& \cos x=\frac{d t}{d x} \\
& \Rightarrow \cos x d x=d t \\
& \text { for } x=0, t=0 \\
& x=\frac{\pi}{2}, t=1
\end{aligned}
$$
$$
I=2 \int_0^1 t \tan _I^{-1}(t) d t
$$

Using integration by parts
$$
I=2\left[\tan ^{-1} t \cdot \frac{t^2}{2}-\int \frac{1}{t^2+1} \cdot \frac{t^2}{2} d t\right]_0^1
$$

$$
\begin{aligned}
I= & 2\left[\tan ^{-1} t \cdot \frac{t^2}{2}-\int \frac{1}{t^2+1} \cdot \frac{t^2}{2} d t\right]_0^1 \\
= & 2\left[\frac{t^2}{2} \tan ^{-1} t-\frac{1}{2} \int \frac{\left(t^2+1\right)-1}{t^2+1} d t\right]_0^1 \\
= & 2\left[\frac{t^2}{2} \tan ^{-1} t-\frac{1}{2} \int d t+\frac{1}{2} \int \frac{1}{t^2+1} d t\right]_0^1 \\
= & 2\left[\frac{t^2}{2} \tan ^{-1} t-\frac{1}{2} t+\frac{1}{2} \tan ^{-1} t\right]_0^1 \\
= & 2\left[\frac{1}{2} \tan ^{-1}(1)-\frac{1}{2}+\frac{1}{2} \tan ^{-1}(1)\right] \\
& -2\left[0 \tan ^{-1}(0)-\frac{1}{2}(0)+\frac{1}{2} \tan ^{-1}(0)\right] \\
= & 2\left[\frac{1}{2} \cdot \frac{\pi}{4}-\frac{1}{2}+\frac{1}{2} \frac{\pi}{4}\right] \\
= & 2\left[\frac{\pi}{4}-\frac{1}{2}\right] \\
& =\frac{\pi}{2}-1
\end{aligned}
$$

Q. 31.NCERT Class 12 Maths Misc. Ex. Ch 7 (Definite Integrals)

$$
I=\int_{1}^{4}\big(|x-1|+|x-2|+|x-3|\big)\,dx
$$

$$
|x-1|=
\begin{cases}
x-1 & x\ge1
\end{cases}
$$

$$
|x-2|=
\begin{cases}
2-x & 1\le x<2 \\
x-2 & x\ge2
\end{cases}
$$

$$
|x-3|=
\begin{cases}
3-x & 1\le x<3 \\
x-3 & x\ge3
\end{cases}
$$

$$
I=\int_{1}^{2}\big((x-1)+(2-x)+(3-x)\big)\,dx\\
+\int_{2}^{3}\big((x-1)+(x-2)+(3-x)\big)\,dx\\
+\int_{3}^{4}\big((x-1)+(x-2)+(x-3)\big)\,dx
$$

$$
\begin{aligned}
& =\int_1^2(4-x) d x+\int_2^3 x d x+\int_3^4(3 x-6) d x \\
& =\left[4 x-\frac{x^2}{2}\right]_1^2+\left[\frac{x^2}{2}\right]_2^3+\left[\frac{3 x^2}{2}-6 x\right]_3^4 \\
& =\left[(8-2)-\left(4-\frac{1}{2}\right)\right]+\left[\frac{9}{2}-2\right]+\left[(24-24)-\left(\frac{27}{2}-18\right)\right. \\
& =\left[6-\frac{7}{2}\right]+\frac{5}{2}+\frac{9}{2}=\frac{19}{2} .
\end{aligned}
$$

Prove the following (Exercises 32 to 37)

Q. 32. NCERT Class 12 Maths Misc. Ex. Ch 7 (Definite Integrals)

$$
\begin{aligned}
& I=\int_1^3 \frac{d x}{x^2(x+1)}=\frac{2}{3} \log \frac{2}{3} \\
& \frac{1}{x^2(x+1)}=\frac{A}{x+1}+\frac{B x+C}{x^2} \\
& 1=A x^2+(B x+C)(x+1) \\
& 1=A x^2+B x^2+(B+C) x+C \\
& 1=(A+B) x^2+(B+C) x+C
\end{aligned}
$$

Eqnating both sides,
$$
\begin{array}{rl}
& C=1, \quad B+C=0 \\
\Rightarrow & B=-C=-1 \\
\Rightarrow & B=-1 \\
A+B=0 & A=-B \\
\Rightarrow & A=1, B=-1, C=1 \\
I= & \int_1^3\left [\frac{1}{x+1}-\frac{x+1}{x^2}\right] d x \\
= & \int_1^3 \frac{1}{x+1} d x-\int_1^3 \frac{1}{x} d x+\int_1^3 \frac{1}{x^2} d x \\
= & {[\log |x+1|] _1^3-[\log x]_1^3+\left [\frac{1}{x}\right] _1^3}
\end{array}
$$

$$
\begin{aligned}
= & {[\log (3+1)-\log (1+1)] } \\
& -[\log 3-\log 1]-\left(\frac{1}{3}-1\right) \\
= & \log \frac{4}{2}-\log 3+0+\frac{2}{3} \\
= & \log \frac{2}{3}+\frac{2}{3}
\end{aligned}
$$

Q. 33. Solution

$$
\begin{aligned}
I & =\int_0 x e^x d x=1 \\
L H S & =\left[x e^x-\int 1 \cdot e^x d x\right]_0^1 \\
& =\left[x e^x-e^x\right]_0^1 \\
& =(1 \cdot e-e)-\left(0 \cdot e^0-e^0\right) \\
& =0-(0-1) \\
& =1 \\
& \text { proved }
\end{aligned}
$$

IMPORTANT QUESTIONS OF NCERT (CBSE) FOR 12TH BOARD 2026

Q. 34. Solution:

$$
\begin{aligned}
&\int_{-1}^1 x^{17} \cos ^4 x d x=0\\
&\begin{aligned}
\text { Let } f(x)= & x^{17} \cos ^4 x \\
\Rightarrow f(-x)= & (-x)^{17}[\cos (-x)]^4 \\
= & -x^{17} \cos ^4 x \\
= & -f(x)
\end{aligned}\\
&\text { Using } \int_{-a}^a f(x)=0 \text { if } f(-x)=-f(x)\\
& \quad \int_{-1}^1 x^{17} \cos ^4 x d x=0
\end{aligned}
$$

Q. 35. Solution:

$$
\begin{aligned}
&\begin{aligned}
& \int_0^{\pi / 2} \sin ^3 x d x=\frac{2}{3} \\
& L H S=\int_0^{\frac{\pi}{2}} \sin ^2 x \cdot \sin x d x \\
& =\int_0^{\frac{\pi}{2}}\left(1-\cos ^2 x\right) \sin x d x \\
& \text { Put } \cos x=t \\
& \text { diff.w.r.t.x } \\
& -\sin x=\frac{d t}{d x} \\
& \sin x d x=-d t \\
& \omega h e n x=0, t=1 \\
& x=\frac{\pi}{2}, t=0 \\
& =\int_1^0\left(1-t^2\right) d t \\
& =\int_0^1\left(1-t^2\right) d t \\
& =\left[t-\frac{t^3}{3}\right]_0^1 \\
& =\left(1-\frac{1}{3}\right)-(0-0) \\
& =\frac{2}{3}=R H S
\end{aligned}\\
&\text { Hence Proved }
\end{aligned}
$$

Q. 36. Solution:

$$
\begin{aligned}
&\begin{aligned}
\int_0^{\frac{\pi}{4}} 2 \tan ^3 x d x & =1-\log 2 \\
\operatorname{LH} S & =2 \int_0^{\frac{\pi}{4}} \tan ^2 x \cdot \tan x d x \\
& =2 \int_0^{\frac{\pi}{4}}\left(\sec ^2 x-1\right) \tan x d x \\
& =2\left[\int_0^{\frac{\pi}{4}} \sec ^2 x \tan x d x-\int_0^{\frac{\pi}{4}} \tan x d x\right] \\
& \begin{array}{l}
\rho \cot \tan x=t \\
\Rightarrow \sec ^2 x d x=d t \\
x=0, t=0 \\
x=\frac{\pi}{4}, t=1
\end{array} \\
& =2\left[\begin{array}{l}
\int_0^t d t-[\log \sec x]_0^{\pi / 4} \\
-2\left[\left(\frac{t^2}{2}\right)_0^1-\left[\log \sec \frac{\pi}{4}-\log \sec 0\right]\right.
\end{array}\right] \\
& =2\left[\frac{1}{2}-(\log \sqrt{2}-\log 1)\right] \\
& =2\left[\frac{1}{2}-\left(\frac{1}{2} \log 2-0\right)\right] \\
& =1-\log 2=R H S
\end{aligned}\\
&\text { proved }
\end{aligned}
$$

Q. 37. Solution

$$
\begin{aligned}
& \int_0^1 \sin ^{-1} x d x=\frac{\pi}{2}-1 \\
& L H S=\int_0^1 1 \cdot \sin ^{-1} x d x \\
& =\left[\sin ^{-1} x \cdot(x)\right]_0^1-\int_0^1 \frac{1}{\sqrt{1-x^2}} \cdot x d x \\
& =\sin ^{-1}(1) \cdot(1)-\sin ^{-1}(0)-\int_0^1 \frac{x}{\sqrt{1-x^2}} d x \\
& =\frac{\pi}{2}-I_1 \cdots \cdots(1) \\
& I_1=\int_0^1 \frac{x}{\sqrt{1-x^2}} d x \\
& P u t t=1-x^2=t \\
& d \cdot f f \cdot \omega \cdot r \cdot t \cdot x \\
& -2 x d x=d t \\
& x d x=-\frac{1}{2} d t \\
& I f x=0, t=1 \\
& x=1, t=0 \\
& 0 \\
& I_1=\frac{-1}{2} \int_1^0 \frac{d t}{\sqrt{x}}=\frac{1}{2} \int_0^1 \frac{d t}{\sqrt{x}} \\
& =\frac{1}{2} \cdot 2[\sqrt{t}]_0^1 \\
& =(\sqrt{1}-0)=1
\end{aligned}
$$

From (1)
$$
\text { LHS }=\frac{\pi}{2}-1=\text { RHS }
$$

Hence proved.

Choose the correct answers in Exercises 38 to 40

Q. 38. solution

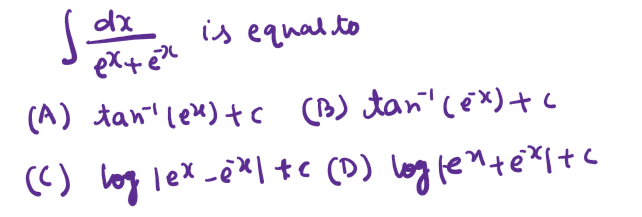
Solution:
$$
\int \frac{d x}{e^x+e^{-x}}
$$

Multiplying Num. and den.by $e^x$
$$
\int \frac{e^x d x}{e^{2 x}+1}
$$

Put $e^x=t$
$$
\begin{aligned}
& \Rightarrow e^x d x=d t \\
& \int \frac{d t}{t^2+1}=\tan ^{-1} t+c \\
& =\tan ^{-1}\left(e^x\right)+c
\end{aligned}
$$

Ans. (A)

Q. 39. solution:

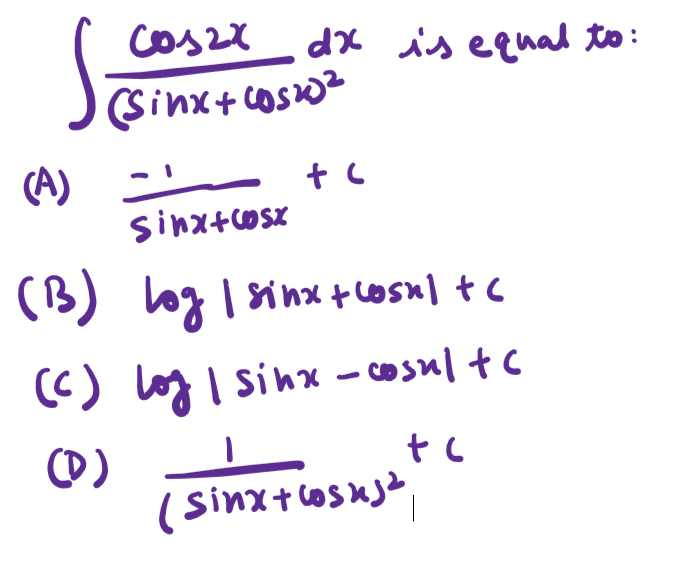
$$\int \frac{\cos 2 x}{(\sin x+\cos x)^2} d x
$$
\begin{aligned}
& =\int \frac{\left(\cos ^2 x-\sin ^2 x\right)}{(\cos x+\sin x)^2} d x \\
& =\int \frac{(\cos x+\sin x)(\cos x-\sin x)}{(\cos x+\sin x)^2} d x \\
& =\int \frac{\cos x-\sin x}{\cos x+\sin x} d x
\end{aligned}
$$

Put $\cos x+\sin x=l$
$$
\begin{aligned}
\text { diff. } \omega \cdot r \cdot t \cdot x & \\
& -\sin x+\cos x=\frac{d t}{d x} \\
\Rightarrow & (\cos x-\sin x) d x=d t \\
= & \int \frac{d t}{t}=\log t+c \\
= & \log |\sin x+\cos x|+c
\end{aligned}
$$

Ans. (B)

Q. 40. Solution

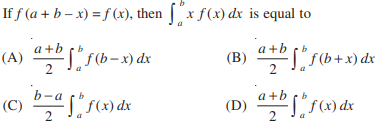
$$
\begin{aligned}
&\begin{aligned}
I & =\int_a^b x f(x) d x \\
& =\int_a^b(\overline{a+b}-x) f(a+b-x) d x \\
& =\int_a^b(a+b) f(x) d x-\int_a^b x f(x) d x \\
I & =(a+b) \int_a^b f(x) d x-I \\
2 I & =(a+b) \int_a^b f(x) d x \\
I & =\frac{a+b}{2} \int_a^b f(x) d x
\end{aligned}\
&\text { Ans. (D) }
\end{aligned}
$$

Free Download Assignment for Practice on Indefinite Integrals