NCERT Class 12 maths Misc. ex. ch. 10 Q. 1. Solution

Free NCERT Class 12 maths Miscellaneous Ex. Chapter 10 Solution PDF Download

Q.1. NCERT Class 12 maths Misc. ex. ch. 10

$$
\textbf{1. Write down a unit vector in XY-plane, making an angle of }30^\circ
\text{ with the positive direction of x-axis}
$$

$$
\text{The unit vector in XY plane is} \

\begin{aligned}
&\text { The unit vector in } \mathrm{XY} \text { plane is } \cos 30 \mathrm{i}+\cos 60^0 j\
&=\frac{\sqrt{3}}{2} \hat{i}+\frac{1}{2} \hat{j}
\end{aligned}

Q.2. NCERT Class 12 maths Misc. ex. ch. 10

$$
\textbf{2. Find the scalar components and magnitude of the vector joining the points }
P(x_1, y_1, z_1)\ \text{and}\ Q(x_2, y_2, z_2).
$$

$$
\text{Solution: Scalar components: }(x_2 – x_1),\ (y_2 – y_1),\ (z_2 – z_1)
$$

$$
\text{Vector Component: }(x_2 – x_1)\mathbf{i} + (y_2 – y_1)\mathbf{j} + (z_2 – z_1)\mathbf{k}
$$

Q.3. NCERT Class 12 maths Misc. ex. ch. 10

$$
\textbf{3. A girl walks 4 km towards the west, then she walks 3 km in a direction }
30^\circ\ \text{east of north and stops. Determine the girl’s displacement.}
$$

$$
\text{Solution:}
$$

$$
\text{To find: Displacement}
$$

$$
\begin{aligned}
&\overrightarrow{AB} \
&\overrightarrow{OA} = 4(\cos 0^\circ\, \mathbf{i} + \cos 90^\circ\, \mathbf{j}) \\
&\overrightarrow{OA} = 4\mathbf{i} \\
&\overrightarrow{OB} = 3(\cos 60^\circ\, \mathbf{i} + \cos 30^\circ\, \mathbf{j}) \\
&\overrightarrow{OB} = \frac{3}{2}\mathbf{i} + \frac{3\sqrt{3}}{2}\mathbf{j} \\
&\overrightarrow{AB} = \overrightarrow{OB} – \overrightarrow{OA} \\
&\overrightarrow{AB} = \left(\frac{3}{2} – 4\right)\mathbf{i} + \frac{3\sqrt{3}}{2}\mathbf{j} \\
&\overrightarrow{AB} = \left(-\frac{5}{2}\right)\mathbf{i} + \frac{3\sqrt{3}}{2}\mathbf{j}
\end{aligned}
$$

YOU MAY ALSO LIKE👇

1. NCERT Maths Ch 6 Misc. Ex. solution. 2. Free NCERT Class 12 Maths Miscellaneous Ex. Ch 7 Solution

Q.4. NCERT Class 12 maths Misc. ex. ch. 10

$$
\textbf{Q.4. } \text{If } \vec{a} = \vec{b} + \vec{c} \text{ then is it true that } |\vec{a}| = |\vec{b}| + |\vec{c}|? \text{ Justify your answer.}
$$

$$
\text{Solution: } |\vec{a}| = |\vec{b} + \vec{c}| \
|\vec{a}| \neq |\vec{b}| + |\vec{c}| \
\text{Hence, the given statement is not true.}
$$

NCERT Class 12 maths Misc. ex. ch. 10

$$
\textbf{Q.5. Find the value of } x \text{ for which } x(\mathbf{i}+\mathbf{j}+\mathbf{k}) \text{ is a unit vector.}
$$

$$
\text{Let } \vec{a} = \mathbf{i} + \mathbf{j} + \mathbf{k} \
|\vec{a}| = \sqrt{1^2 + 1^2 + 1^2} = \sqrt{3} \
\text{Unit vector } = \frac{\vec{a}}{|\vec{a}|} = \frac{1}{\sqrt{3}}(\mathbf{i}+\mathbf{j}+\mathbf{k})
$$

$$
x(\mathbf{i}+\mathbf{j}+\mathbf{k}) = \frac{1}{\sqrt{3}}(\mathbf{i}+\mathbf{j}+\mathbf{k}) \
\Rightarrow x = \frac{1}{\sqrt{3}}
$$

Q.6. NCERT Class 12 maths Misc. ex. ch. 10

$$
\textbf{Q.6. Find a vector of magnitude 5 units and parallel to the resultant of } \
\vec{a}=2\mathbf{i}+3\mathbf{j}-\mathbf{k},\quad \vec{b}=\mathbf{i}-2\mathbf{j}+\mathbf{k}.
$$

$$
\text{Resultant } \vec{r} = \vec{a} + \vec{b} \
\vec{r} = (2\mathbf{i}+3\mathbf{j}-\mathbf{k}) + (\mathbf{i}-2\mathbf{j}+\mathbf{k}) \
\vec{r} = 3\mathbf{i} + \mathbf{j}
$$

$$
|\vec{r}| = \sqrt{3^2 + 1^2} = \sqrt{10}
$$

$$
\text{Required vector} = 5 \cdot \frac{\vec{r}}{|\vec{r}|}
= 5 \cdot \frac{3\mathbf{i}+\mathbf{j}}{\sqrt{10}}
$$

$$
= \frac{15}{\sqrt{10}}\mathbf{i} + \frac{5}{\sqrt{10}}\mathbf{j}
= \frac{3\sqrt{10}}{2}\mathbf{i} + \frac{\sqrt{10}}{2}\mathbf{j}
$$

Q. 7. NCERT Class 12 maths Misc. ex. ch. 10

Q. 7. If , find a unit vector parallel to the vector

Solution:

Now unit vector parallel to this vector

Q.8. NCERT Class 12 maths Misc. ex. ch. 10

$$
\textbf{Q.8. Show that the points } A(1,-2,-8),\; B(5,0,-2),\; C(11,3,7) \text{ are collinear.}
$$

$$
\vec{AB} = (5-1)\mathbf{i} + (0+2)\mathbf{j} + (-2+8)\mathbf{k}
= 4\mathbf{i} + 2\mathbf{j} + 6\mathbf{k}
$$

$$
\vec{BC} = (11-5)\mathbf{i} + (3-0)\mathbf{j} + (7+2)\mathbf{k}
= 6\mathbf{i} + 3\mathbf{j} + 9\mathbf{k}
$$

$$
\frac{4}{6} = \frac{2}{3} = \frac{6}{9} \
\Rightarrow A, B, C \text{ are collinear.}
$$

$$
\text{Ratio in which B divides AC} = \frac{2}{3}
$$

Q. 9. NCERT Class 12 maths Misc. ex. ch. 10

$$
\textbf{Q.9. Position vector of point R dividing PQ externally in the ratio }1:2, \
\vec{OP} = 2\vec{a}+\vec{b},\; \vec{OQ} = 3\vec{a}-\vec{b}.
$$

$$
\vec{OR} = \frac{1\cdot\vec{OQ} – 2\cdot\vec{OP}}{1-2}
$$

$$
= \frac{(3\vec{a}-\vec{b}) – 2(2\vec{a}+\vec{b})}{-1}
$$

$$
= \frac{3\vec{a}-\vec{b}-4\vec{a}-2\vec{b}}{-1}
= \vec{a} + 3\vec{b}
$$

$$
\text{Check if P is midpoint of RQ: } \
\vec{OP} = \frac{\vec{OR} + \vec{OQ}}{2}
$$

$$
\frac{(\vec{a}+3\vec{b}) + (3\vec{a}-\vec{b})}{2}
= \frac{4\vec{a} + 2\vec{b}}{2}
= 2\vec{a} + \vec{b}
$$

$$
\text{Hence proved.}
$$

Q.10. NCERT Class 12 maths Misc. ex. ch. 10

$$
\textbf{Q.10. Adjacent sides of a parallelogram are } \vec{a}=2\mathbf{i}-4\mathbf{j}+5\mathbf{k},\;
\vec{b}=\mathbf{i}-2\mathbf{j}-3\mathbf{k}. \
\text{Find unit vector parallel to diagonal and its area.}
$$

Solution:
Area of a parallelogram is the magnitude of Cross (Vector) Product of adjacent sides.
Let
Then area of the parallelogram

$$
= \mathbf{i}(12 – (-10)) – \mathbf{j}(-6 – 5) + \mathbf{k}(-4 + 4)
$$

$$
= 22\mathbf{i} + 11\mathbf{j}
$$

$$
|\vec{a} \times \vec{b}|
= \sqrt{22^2 + 11^2}
= \sqrt{484 + 121}
= \sqrt{605}
$$

Q. 11. NCERT Class 12 maths Misc. ex. ch. 10

Q.11. Show that the direction cosines of a vector equally inclined to OX, OY and OZ are 1/sqrt3, 1/sqrt3, 1/sqrt3.

Let the direction cosines be $\cos\alpha, \cos\beta, \cos\gamma$.

Since they are equally inclined:

$$
\cos\alpha = \cos\beta = \cos\gamma
$$

Using the identity:

$$
\cos^2\alpha + \cos^2\beta + \cos^2\gamma = 1
$$

So,

$$
3\cos^2\alpha = 1
$$

$$
\cos^2\alpha = \frac{1}{3}
$$

$$
\cos\alpha = \pm\frac{1}{\sqrt{3}}
$$

Therefore the direction cosines are:

$$
\frac{1}{\sqrt{3}},\ \frac{1}{\sqrt{3}},\ \frac{1}{\sqrt{3}}
$$

Q. 12.NCERT Class 12 maths Misc. ex. ch. 10

Q. 12. Let . Find a vector  which is perpendicular to both  and and.
Solution:
Since is perpendicular to both  and .
Therefore,

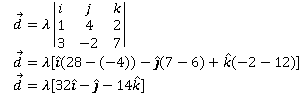
Now, .

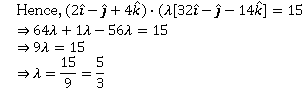
Therefore,

Q. 13. NCERT Class 12 maths Misc. ex. ch. 10

Q. 13. The scalar product of the vector i+j+k with a unit vector along the sum of vectors 2i+4j-5k and i+2j+3k is equal to one. Find the value of λ.

Solution:

The sum of vectors  and

∴ unit vector
Now dot Product with

Now, .

Therefore,

Q. 14. NCERT Class 12 maths Misc. ex. ch. 10

4. If $\vec{a}, \vec{b}, \vec{c}$ are mutually perpendicular vectors of equal magnitudes,
   show that the vector $\vec{a}+\vec{b}+\vec{c}$ is equally inclined with $\vec{a}, \vec{b}$, and $\vec{c}$.

Solution: We have $|\vec{a}| = |\vec{b}| = |\vec{c}|$ and
$\vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{c} = \vec{c}\cdot\vec{a} = 0$ as they are mutually perpendicular.

Let the angles between $\vec{a}+\vec{b}+\vec{c}$ and $\vec{a}, \vec{b}, \vec{c}$ be
$\alpha, \beta$, and $\gamma$, respectively.

$$
\cos\alpha
= \frac{\vec{a}\cdot(\vec{a}+\vec{b}+\vec{c})}{|\vec{a}|\,|\vec{a}+\vec{b}+\vec{c}|}
$$

$$
= \frac{\vec{a}\cdot\vec{a} + \vec{a}\cdot\vec{b} + \vec{a}\cdot\vec{c}}{|\vec{a}|\,|\vec{a}+\vec{b}+\vec{c}|}
$$

$$
= \frac{|\vec{a}|^2 + 0 + 0}{|\vec{a}|\,|\vec{a}+\vec{b}+\vec{c}|}
= \frac{|\vec{a}|} {|\vec{a}+\vec{b}+\vec{c}|}
$$

Similarly, we can show:

$$
\cos\beta = \frac{|\vec{b}|}{|\vec{a}+\vec{b}+\vec{c}|},\qquad
\cos\gamma = \frac{|\vec{c}|}{|\vec{a}+\vec{b}+\vec{c}|}
$$

$$
\text{But }|\vec{a}| = |\vec{b}| = |\vec{c}|
$$

$$
\therefore\ \cos\alpha = \cos\beta = \cos\gamma
$$

$$
\Longrightarrow\ \alpha = \beta = \gamma
$$

$$
\text{Hence, }(\vec{a}+\vec{b}+\vec{c})\text{ is equally inclined with }\vec{a},\ \vec{b},\ \vec{c}.
$$

$$
\text{Proved.}
$$

Q. 15. NCERT Class 12 maths Misc. ex. ch. 10

$$
\text{Q. 15. Prove that } (\vec{a}+\vec{b})\cdot(\vec{a}+\vec{b}) = |\vec{a}|^{2} + |\vec{b}|^{2}
\text{ if and only if }\vec{a}\perp\vec{b},\ \vec{a}\neq 0,\ \vec{b}\neq 0.
$$

Solution:

$$
(\vec{a}+\vec{b})\cdot(\vec{a}+\vec{b})
$$

$$
= \vec{a}\cdot\vec{a} + \vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{a} + \vec{b}\cdot\vec{b}
$$

$$
= |\vec{a}|^{2} + 0 + 0 + |\vec{b}|^{2}
$$

$$
= |\vec{a}|^{2} + |\vec{b}|^{2}
$$

$$
\text{Proved.}
$$

Q.16. Maths Class 12 Misc Ex Ch 10 soltuon

If $latex \theta$ is the angle between two vectors $latex \vec{a}$ and $latex \vec{b}$, then
$latex \vec{a}\cdot\vec{b} \ge 0$ only when:

(A) $latex 0 < \theta < \frac{\pi}{2}$
(B) $latex 0 \le \theta \le \frac{\pi}{2}$
(C) $latex 0 < \theta < \pi$
(D) $latex 0 \le \theta \le \pi$

Solution:

\[
\cos\theta = \frac{\vec{a}\cdot\vec{b}}{\lvert \vec{a} \rvert, \lvert \vec{b} \rvert}
\]

If $latex \vec{a}\cdot\vec{b} \ge 0$, then $latex \cos\theta \ge 0$.

\[
0 \le \theta \le \frac{\pi}{2}
\]

Ans. (B)

Q. 17. NCERT misc ex ch 10 class 12 maths solution

Q.17. Let ( \vec{a} ) and ( \vec{b} ) be two unit vectors and ( \theta ) is the angle between them.
Then ( \vec{a} + \vec{b} ) will be a unit vector if

(A) ( \theta = \pi/4 )
(B) ( \theta = \pi/3 )
(C) ( \theta = \pi/2 )
(D) ( \theta = 2\pi/3 )

Solution:

$$
|\vec{a} + \vec{b}|^{2}
= |\vec{a}|^{2} + |\vec{b}|^{2} + 2|\vec{a}||\vec{b}|\cos\theta
$$

$$
|\vec{a}| = |\vec{b}| = 1
$$

$$
\Rightarrow 1 = 1 + 1 + 2\cos\theta
$$

$$
\Rightarrow \cos\theta = -\frac{1}{2} \Rightarrow \theta = \frac{2\pi}{3}
\quad \text{Ans. (D)}
$$

---

Q.18. NCERT Solution Class 12 Maths Misc. Ex. Ch-10

The value of

\[
\vec{i}\cdot(\vec{j}\times\vec{k}) +
\vec{j}\cdot(\vec{i}\times\vec{k}) +
\vec{k}\cdot(\vec{i}\times\vec{j})
\]

is:

(A) $latex 0$
(B) $latex -1$
(C) $latex 1$
(D) $latex 3$

Solution:

\[
\vec{j}\times\vec{k}=\vec{i},\quad
\vec{k}\times\vec{i}=\vec{j},\quad
\vec{i}\times\vec{j}=\vec{k}
\]\[
\vec{i}\cdot\vec{i}

• \vec{j}\cdot\vec{j}

• \vec{k}\cdot\vec{k}
  = 1 + 1 + 1 = 3
  \]

  Ans. (C)

  Q. 19. NCERT Solution Class 12 Maths Misc. Ex. Ch-10

  Q.19. If ( \theta ) is the angle between any two vectors ( \vec{a} ) and ( \vec{b} ),
  then ( \vec{a} \cdot \vec{b} = \vec{a} \times \vec{b} ) when ( \theta ) is equal to

  (A) ( 0 )
  (B) ( \pi/4 )
  (C) ( \pi/2 )
  (D) ( \pi )

  Solution:

  We have,

  $$
  \vec{a} \cdot \vec{b} = a b \cos\theta
  $$

  $$
  \vec{a} \times \vec{b} = a b \sin\theta
  $$

  $$
  ab\cos\theta = ab\sin\theta
  $$

  $$
  \cos\theta = \sin\theta
  $$

  $$
  \theta = \pi/4
  $$

  Ans. (B).