NCERT Class 12 Maths Chapter 13 (Probability)

Q.1. NCERT Class 12 Maths Ch 13 (Probability) Solution
Q. 1. A and B are two events such that P (A) ≠ 0. Find P(B|A), if (i) A is a subset of B (ii) A ∩ B = φ
Solution:
(i) A is a subset of B.
We have, \begin{array}{{>{\displaystyle}l}}
\ A\ \subset \ B\ \Longrightarrow A\cap B=A\\
Hence,\ P( B/A) =\frac{P( A\cap B)}{P( A)} =\frac{P( A)}{P( A)} =1\\
( ii) \ A\cap B=\phi \Longrightarrow P( A\cap B) =0\\
Hence,\ P( B/A) =\frac{0}{P( A)} =0\\
\end{array}
Q.2. NCERT Class 12 Maths Ch 13 (Probability) Solution
Q.2. A couple has two children,
(i) Find the probability that both children are males, if it is known that at least
one of the children is male.
(ii) Find the probability that both children are females, if it is known that the
elder child is a female.
Solution:
$\displaystyle \begin{array}{{>{\displaystyle}l}}
( i) \ Both\ children\ are\ males\\
S={BB,BG,GB,GG}\\
E=Both\ childeren\ are\ males\\
={BB}\\
F=At\ least\ one\ of\ the\ children\ is\ male\\
={BB,BG,GB}\\
P( E) =\frac{1}{4}\\
P( F) =\frac{3}{4}\\
P( E\cap F) =\frac{1}{4}\\
P( E/F) =\frac{P( E\cap F)}{P( F)}\\
P( E/F) =\frac{\frac{1}{4}}{\frac{3}{4}} =\frac{1}{3}\\
Ans.\ \frac{1}{3}\\
\end{array}
(ii) Find the probability that both children are females, if it is known that the
elder child is a female.
\begin{array}{l}
Let\ E=\ Both\ childeren\ are\ females\
F=\ Elder\ child\ is\ a\ female\
P( E) =\frac{1}{ \begin{array}{l}
4\\
\end{array}}\
P( F) =\frac{2}{4}\\
P( E\cap F) =\frac{1}{4}\\
P( E/F) =\frac{P( E\cap F)}{P( F)}\\
=\frac{\frac{1}{4}}{\frac{2}{4}} =\frac{1}{2}
\end{array}
Q.3. NCERT Class 12 Maths Ch 13 (Probability) Solution
Q.3. Suppose that 5% of men and 0.25% of women have grey hair. A grey haired
person is selected at random. What is the probability of this person being male?
Assume that there are equal number of males and females.
Solution:
\begin{array}{{>{\displaystyle}l}}
Let\ M=\ Number\ of\ males,\ F=\ Number\ of\ females.\\
G=\ Having\ grey\ hair.\\
P( M) =\ 0.5\ \ \ P( F) =0.5\\
P( G/M) =0.05\ \ \ \ \ \ \ \ \ \ \ P( G/F) =0.0025\\
Using\ Baye’s\ Theorem,\\
P( M/G) =\frac{P( G/M) P( M)}{P( G/M) P( M) +P( G/F) P( F)}\\
=\frac{0.5\times 0.05}{0.5\times 0.05+0.5\times 0.0025}\\
=\frac{0.025}{0.025+0.00125} =\frac{20}{21}\\
Ans.\ \frac{20}{21}
\end{array}
Q.4. NCERT Class 12 Maths Ch 13 (Probability) Solution
Q.4. Suppose that 90% of people are right-handed. What is the probability that
at most 6 of a random sample of 10 people are right-handed?
Solution:
$\displaystyle \begin{array}{{>{\displaystyle}l}}
Let\ E=Peoplr\ are\ right\ handed.\ F=People\ who\ are\ not\ right\ handed.\
P( E) =0.9,\ P( E’) =0.1\ No.\ of\ people\ ( n) =10\
No.\ of\ people\ having\ right\ handed\ ( r) \ ={0,1,2,3,4,5,6}\
P( At\ most\ 6\ people\ out\ of\ 10\ people\ are\ right\ handed) =\ \sum {r=0}^{6} 10{C}{}_{r}( 0.9)^{r}( 0.1)^{10-r}\
\end{array}$
Q. 5. NCERT Class 12 Maths Ch 13 (Probability) Solution
Q. 5. If a leap year is selected at random, what is the chance that it will contain 53
tuesdays?
Solution:
In a leap year, there are 366 days= 52 weeks + 2odd days.
Out of these 2 days the probability of having 1 Tuesday for 53 Tuesdays= 2/7
Ans. 2/7

Q.6. NCERT Class 12 Maths Ch 13 (Probability) Solution
Q.6. Suppose we have four boxes A,B,C and D containing coloured marbles as given
below:
| BOX | Marble Colour | Marble Colour | Marble Colour |
| Red | White | Black | |
| A | 1 | 6 | 3 |
| B | 6 | 2 | 2 |
| C | 8 | 1 | 1 |
| D | 0 | 6 | 4 |
One of the boxes has been selected at random and a single marble is drawn from
it. If the marble is red, what is the probability that it was drawn from box A?, box B?,
box C?
Solution:
Let A= Selecting Box A and found to be red
B= Selecting Box B and found to be red.
C=Selecting Box C and found to be red.
P(A)=$\displaystyle \begin{array}{{>{\displaystyle}l}}
\frac{1}{15} \ ,\ as\ total\ no.\ of\ red\ marbles\ =15\ and\ in\ box\ A=1\
\end{array}$
P(B)=$\displaystyle \begin{array}{{>{\displaystyle}l}}
\frac{6}{15} =\frac{2}{5}\
\end{array}$
P(C)=$\displaystyle \frac{8}{15}$ since, no. of red marble in C=8 and Total no. of marbles=15

You May Also Like 👉
Q.7. NCERT Maths Class 12 solutions
Q. 7. Assume that the chance of a patient having a heart attack is 40%. It is also
assumed that a meditation and yoga course reduce the risk of heart attack by
30%, and the prescription of certain drug reduces its chances by 25%. At a time a
The patient can choose any one of the two options with equal probabilities. It is given
that after going through one of the two options the patient selected at random
suffers a heart attack. Find the probability that the patient followed a course of
meditation and yoga?
Solution:
Let $\displaystyle E_{1} =\ The\ patient\ chooses\ yoga\ and\ meditation.$
$\displaystyle \begin{array}{{>{\displaystyle}l}}
E_{2} =\ The\ patient\ takes\ drugs\ and\ medicines.\\
A=The\ patient\ suffers\ with\ Heart-attack.\\
P( E_{1}) =\frac{1}{2} \ =0.5\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P( E_{2}) =\frac{1}{2} =0.5\\
P( A/E_{1}) =\frac{40}{100} \times \left(\frac{100-30}{100}\right) \ \ \ \ \ \ P( A/E_{2}) =\frac{40}{100} \times \left(\frac{100-25}{100}\right)\\
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =0.28\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =0.30\ \\
We\ need\ to\ find\ P( E_{1} /A) .\\
P( E_{1} /A) =\frac{P( E_{1}) \times P( A/E_{1})}{P( E_{1}) \times P( A/E_{1}) +P( E_{2}) \times P( A/E_{2})}\\
=\ \frac{0.5\times 0.28}{0.5\times 0.28+0.5\times 0.30} =\frac{0.28}{0.58} =\frac{14}{ \begin{array}{{>{\displaystyle}l}}
29\
\end{array}}\
Ans.\ \frac{14}{29}\
\end{array}
Q.8. NCERT Class 12 Maths Misc Ex ch 13 Solution
Q.8. If each element of a second-order determinant is either zero or one, what is the
probability that the value of the determinant is positive? (Assume that the individual entries of the determinant are chosen independently, each value being assumed with probability 1/2.)
Solution:
We have second order determinant with entries (0,1). Total number of elements in second order determinant= 2
So, total number of possible determinants with these 2 entries 0 and 1 = \math-container{2\power{4}=16.}
Let E be the event with the value of the determinant to be positive.
If we have determinant
\begin{vmatrix}
a & b\
c & d
\end{vmatrix} \ then\ det=ad-bc >0$
$\displaystyle \begin{vmatrix}
a & b\
c & d
\end{vmatrix} \ then\ det=ad-bc >0$
\begin{array}
ad >bc\ then\ ad=1\Longrightarrow a=1,d=1\ and\ out\ of\ b\ and\ c\ at\ least\ one\ be\ 0.\\
So,\ we\ have\ 3\ possible\ determinants\ with\ positive\ values\ which\ should\ inclue\ a=1,\ b=0\\
or\ c=0\ or\ either\ b=0\&c=1or\ b=1\ \&\ c=0.\\
n( E) =3\\
n( S) =16\\
\
P( E) =\frac{3}{16}\\
Ans.\ \frac{3}{16} .
\end{array}$
Q.9. NCERTClass 12 Maths Misc Ex ch 13 Solution
Q.9. An electronic assembly consists of two subsystems, say, A and B. From previous testing procedures, the following probabilities are assumed to be known:
P(A fails) = 0.2
P(B fails alone) = 0.15
P(A and B fail) = 0.15
Evaluate the following probabilities
(i) P(A fails|B has failed) (ii) P(A fails alone)
\begin{array}{l}
( i) \ P( Afails/B\ has\ failed) =\frac{P( A\cap B)}{P( B)}\\
So,\ first\ we\ have\ to\ find\ P( B)\\
We\ have,\ \
P( B\ fails\ alone) =P( B) -P( A\cap B)\\
0.15=P( B) -0.15\\
So,\ P( B) =0.15+0.15=0.30\\
\Longrightarrow P( Afails/B\ has\ failed) =\frac{P( A\cap B)}{P( B)}\\
=\frac{0.15}{0.30} =0.5\\
( ii) \ P( A\ fails\ alone) =P( A) -P( A\cap B)\\
=0.2-0.15=0.05\
\end{array}
Q.10. NCERT Class 12 Maths Misc Ex Ch 13 Probability Solution
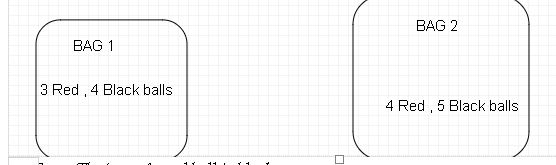
Q. 10. Bag I contains 3 red and 4 black balls and Bag II contains 4 red and 5 black balls.
One ball is transferred from Bag I to Bag II and then a ball is drawn from Bag II.
The ball so drawn is found to be red in colour. Find the probability that the
transferred ball is black.
Solution:
\begin{array}{l}
Let\ E_{1} =\ The\ transferred\ ball\ is\ black.\
E_{2} =The\ transferred\ ball\ is\ red.\\
A=\ The\ ball\ drawn\ from\ the\ bag\ 2\ is\ red.\\
P( E_{1}) =\frac{4}{7} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P( E_{2}) =\frac{3}{7}\\
P( A/E_{1}) =\ \frac{4}{10} \ \ \ \ \ \ \ P( A/E_{2}) =\frac{5}{10}\\
So,\ P( E_{1} /A) =\ \frac{P( E_{1}) \times P( A/E_{1})}{P( E_{1}) \times P( A/E_{1}) +P( E_{2}) \times P( A/E_{2})}\\
\Longrightarrow P( E_{1} /A) =\frac{\frac{4}{7} \times \frac{4}{10}}{\frac{4}{7} \times \frac{4}{10} +\frac{3}{7} \times \frac{5}{10}} =\frac{\frac{16}{70}}{\frac{31}{70}} =\frac{16}{31}\\
Ans.\ \frac{16}{31} .
\end{array}
Q. 11. NCERT Class 12 Maths Ch 13 (Probability) Solution
Q.11. If A and B are two events such that P(A) ≠ 0 and P(B | A) = 1, then
(A) A ⊂ B (B) B ⊂ A (C) B = φ (D) A = φ
Solution:
\begin{array}{l}
P( B/A) =\frac{P( A\cap B)}{P( A)}\\
If\ ( A) \ A\subset B\ then,\ P( B/A) =P( A) /P( A) \ =1\\
Hence,\ Ans.\ ( A) .
\end{array}
Q.12. NCERT Class 12 Maths Misc. Ex. Ch 13
Q.12. If P(A|B) > P(A), then which of the following is correct :
(A) P(B|A) < P(B) (B) P(A ∩ B) < P(A) . P(B)
(C) P(B|A) > P(B) (D) P(B|A) = P(B)
Given:
P(A∣B)>P(A)
Using the definition of conditional probability,
P(A∣B)=P(B)P(A∩B)
So,
P(B)P(A∩B)>P(A)
Multiplying both sides by P(B) (where P(B)>0),
P(A∩B)>P(A)P(B)
Now,
P(B∣A)=P(A)P(A∩B)
Since P(A∩B)>P(A)P(B),
P(A)P(A∩B)>P(B)
That is,
P(B∣A)>P(B)
Correct option: (C)P(B∣A)>P(B)
Q.13 NCERT Class 12 Maths Chapter 13 (Probability) Solution
Q. 13. If A and B are any two events such that P(A) + P(B) – P(A and B) = P(A), then
(A) P(B|A) = 1 (B) P(A|B) = 1
(C) P(B|A) = 0 (D) P(A|B) = 0
Solution:
Given
P(A)+P(B)−P(A∩B)=P(A)
Subtract P(A) from both sides:
P(B)−P(A∩B)=0
So,
P(B)=P(A∩B)
Now,
P(B∣A)=P(A)P(A∩B)=P(A)P(B)
and
P(A∣B)=P(B)P(A∩B)=P(B)P(B)=1
Hence, the correct option is:(B) P(A∣B)=1


